Sigma Notation Guide: Master Math Symbols

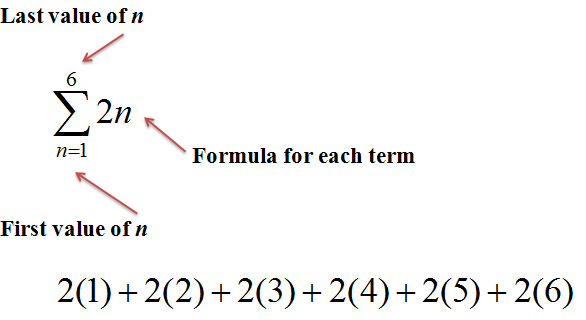
The sigma notation, denoted by the capital letter sigma (Σ), is a mathematical shorthand used to represent a sum of multiple terms. It is a fundamental concept in mathematics, particularly in algebra, calculus, and statistics. In this comprehensive guide, we will delve into the world of sigma notation, exploring its definition, rules, and applications.

Introduction to Sigma Notation

Sigma notation is a concise way to express a sum of terms, making it easier to work with complex mathematical expressions. The notation consists of the sigma symbol, followed by the expression to be summed, and then the limits of summation. The general form of sigma notation is:

Σ (expression) = (first term) + (second term) +… + (last term)

For example, the sum of the first five positive integers can be written as:

Σ (i) from i=1 to 5 = 1 + 2 + 3 + 4 + 5

This can be read as “the sum of i, from i equals 1 to 5.”

Rules of Sigma Notation

To work effectively with sigma notation, it is essential to understand the rules that govern its use. Here are some key rules to keep in mind:

1. The index of summation: The letter used to represent the index of summation is usually i, j, or k. It is essential to choose an index that is not already used in the expression.
2. The limits of summation: The limits of summation are the values that the index takes on. The lower limit is the starting value, and the upper limit is the ending value.
3. The expression to be summed: The expression to be summed is the mathematical expression that is being added up.

Examples of Sigma Notation

To illustrate the concept of sigma notation, let’s consider a few examples:

• Σ (2i) from i=1 to 3 = 2(1) + 2(2) + 2(3) = 2 + 4 + 6 = 12
• Σ (i^2) from i=1 to 4 = 1^2 + 2^2 + 3^2 + 4^2 = 1 + 4 + 9 + 16 = 30
• Σ (3i - 2) from i=1 to 5 = (3(1) - 2) + (3(2) - 2) + (3(3) - 2) + (3(4) - 2) + (3(5) - 2) = 1 + 4 + 7 + 10 + 13 = 35

Properties of Sigma Notation

Sigma notation has several properties that make it a powerful tool for mathematical expressions. Some of these properties include:

• Linearity: The sum of two expressions is equal to the sum of each expression separately.
• Commutativity: The order of the terms in a sum does not affect the result.
• Associativity: The order in which we add terms does not affect the result.

Applications of Sigma Notation

Sigma notation has numerous applications in mathematics, particularly in:

• Algebra: Sigma notation is used to represent sums of terms in algebraic expressions.
• Calculus: Sigma notation is used to represent sums of infinite series, which are essential in calculus.
• Statistics: Sigma notation is used to represent sums of data, which is crucial in statistical analysis.

Conclusion

In conclusion, sigma notation is a powerful mathematical tool that simplifies complex mathematical expressions. By understanding the rules and properties of sigma notation, you can work more efficiently with mathematical expressions and develop a deeper appreciation for the beauty of mathematics.

FAQ Section

Key Takeaways

• Sigma notation is a concise way to represent a sum of multiple terms.
• The rules of sigma notation include choosing an index of summation, specifying the limits of summation, and defining the expression to be summed.
• Sigma notation has numerous applications in mathematics, particularly in algebra, calculus, and statistics.

Decision Framework

When working with sigma notation, consider the following decision framework:

• Identify the index of summation: Choose a letter that is not already used in the expression.
• Specify the limits of summation: Define the starting and ending values of the index.
• Define the expression to be summed: Specify the mathematical expression that is being added up.
• Apply the rules of sigma notation: Use the rules of sigma notation to simplify the expression.

By following this decision framework and understanding the rules and properties of sigma notation, you can work more efficiently with mathematical expressions and develop a deeper appreciation for the beauty of mathematics.