What Is 2Nd Moment Of Area? Calculated Easily
The concept of the 2nd moment of area, also known as the moment of inertia, is a fundamental principle in physics and engineering, particularly in the fields of mechanics, structural analysis, and design. It is a measure of an object’s resistance to changes in its rotation or, in the context of beams and columns, its resistance to bending and torsion. This property is crucial for understanding how structures behave under various loads and for designing them to withstand external forces without failing.
Introduction to the 2nd Moment of Area
The 2nd moment of area, denoted by the symbol I, is calculated with respect to a specific axis. It is defined as the sum of the products of the elemental areas of a shape and the square of their distances from the axis in question. Mathematically, this can be expressed as:
[ I = \int y^2 dA ]
where: - (I) is the 2nd moment of area, - (y) is the distance from the axis of reference to the elemental area (dA), - (dA) is the elemental area of the shape.
This calculation can be simplified for common geometric shapes using established formulas, which are derived by integrating the elemental areas over the entire shape.
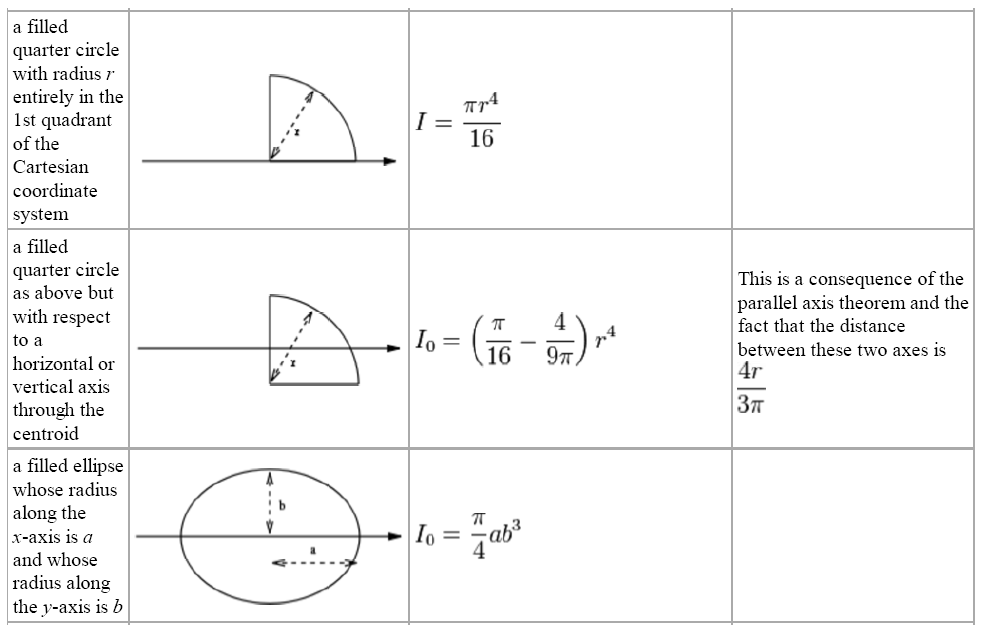
Calculating the 2nd Moment of Area for Common Shapes
Rectangle: For a rectangle, the 2nd moment of area about its neutral axis (the axis passing through the centroid and parallel to the base) is given by: [ I = \frac{bh^3}{12} ] where (b) is the width and (h) is the height of the rectangle.
Circle: For a circular cross-section, the 2nd moment of area about its central axis is: [ I = \frac{\pi d^4}{64} ] where (d) is the diameter of the circle.
Triangle: For a triangular cross-section, about an axis through its vertex and parallel to the base, the formula is: [ I = \frac{bh^3}{36} ] where (b) is the base and (h) is the height of the triangle.
Hollow Tube: The 2nd moment of area for a hollow tube about its central axis can be found by subtracting the moment of inertia of the inner circle from that of the outer circle: [ I = \frac{\pi (D^4 - d^4)}{64} ] where (D) is the outer diameter and (d) is the inner diameter.
Practical Applications and Importance
Understanding and calculating the 2nd moment of area is crucial for a variety of applications, including:
- Structural Engineering: For designing beams, columns, and other structural elements to resist bending and torsion.
- Mechanical Engineering: In the design of shafts, gears, and other machine elements where rotational motion is involved.
- Aerospace Engineering: For analyzing the stability and control of aircraft and spacecraft.
- Civil Engineering: In bridge design, where the 2nd moment of area helps in determining the required size and shape of the structural members to support the anticipated loads.
Calculating the 2nd Moment of Area Easily
To calculate the 2nd moment of area easily, follow these steps: 1. Identify the Shape: Determine the geometric shape of the cross-section. 2. Apply the Formula: Use the appropriate formula for the identified shape. 3. Input Values: Plug in the known dimensions into the formula. 4. Perform Calculation: Calculate the 2nd moment of area using the formula. 5. Verify Units: Ensure that the units of the result are correct (typically mm^4 or m^4).
Example Calculation
Problem: Find the 2nd moment of area about the neutral axis for a rectangular beam with a width of 100 mm and a height of 200 mm.
Solution: [ I = \frac{bh^3}{12} = \frac{100 \times (200)^3}{12} ] [ I = \frac{100 \times 8000000}{12} = \frac{800000000}{12} ] [ I = 66666666.67 \, \text{mm}^4 ]
This example illustrates how to easily calculate the 2nd moment of area for a common shape using the appropriate formula.
In conclusion, the 2nd moment of area is a critical property for understanding the behavior of structures under load and for designing them to be safe and efficient. Calculating it involves applying the correct formula for the shape in question and ensuring that the units are appropriate for the application.


